10. 有向图与偏序

有向图（Digraph） $G$ 由节点组成的 节点集 $V (G)$ 与 有向边 组成的 边集 $E (G)$ 组成，且 $E (G) \subseteq V (G)^{2}$ 。一条有向边可以表示为 $u \to v$ ，其中 $u$ 为这条边的头， $v$ 为这条边的尾。头尾相同的边称作自环。

我们先引入一些与图相关的术语：

每个节点的入度是指以该节点作为尾的边的个数；出度对应是指以该节点作为头的边的个数。显然一张图中所有节点的入度和、出度和均等于有向边的个数。

有向图中的路 $W$ 是一个节点与边交替的序列，始于节点且终于节点。对于路中的每一条边 $e : u \to v$ ，其前驱元素为 $u$ ，后继元素为 $v$ 。该路的长度 $| W |$ 定义为路中的边的个数。若路中经过的任意节点两两不同，称其为通路；若路的起始节点与终止节点相同，称其为回路；若回路中经过的节点除起始节点与终止节点外两两不同，且长度为正，称其为圈。一条路虽然严格定义为节点与边交替的序列，然而其可由边序列唯一决定；当图中无重边时，可由节点序列唯一决定。

当路 $p$ 结束于另一路 $q$ 所起始的节点，可以将两条路合并为一条路，记作 $p \hat{v} q$ ，其中 $v$ 为两路相接的节点。该路的长度等于所接的两路之和。

我们称两张图 $G_{1}$ 与 $G_{2}$ 是 同构（Isomorphic）的，当且仅当存在一个 $V_{1} \to V_{2}$ 的 双射 $f$ ，满足

⟨ u, v ⟩ \in E_{1} \leftrightarrow ⟨ f (u), f (v) ⟩ \in E_{2}

通俗一点讲，如果能够找到一种映射规则，使得映射时任意两顶点间边的邻接关系保持不变，则两张图同构。同构的概念会在 12. 简单图继续讨论。

我们可以用 邻接矩阵 $A_{G}$ 表示一张图。邻接矩阵是一个 $| V | \times | V |$ 的方阵，在不带权的图中，我们简单规定，如果节点 $v_{i}$ 与节点 $v_{j}$ 之间存在一条有限边，赋 $(A_{G})_{i j} = 1$ ，否则为 $0$ ，即

(A_{G})_{i j} = {\begin{cases} 1, & ⟨ v_{i}, v_{j} ⟩ \in E (G) \\ 0, & otherwise \end{cases}

类似地，定义 计数矩阵 $C^{k}$ 记录了图中长度为 $k$ 的路的个数。有定理 $C^{m} C^{n} = C^{m + n}$ ，进一步推论得 $C^{k} = (A_{G})^{k}$ 。特别地， $(A_{G})^{0}$ 为单位阵 $I$ 。

我们定义一个 $V (G)$ 上的二元关系 $G^{*}$ ，称作 路关系，存在路关系 $(u, v)$ ，当且仅当存在一条由 $u$ 到 $v$ 的路。类似有 正路关系 $G^{+}$ ，其要求存在一条长度为正的路；与限定路径长度的 $n$ 长度的路关系 $G^{n}$ ，当且仅当存在一条长为 $n$ 的路。仿照计数矩阵的性质，我们可以证明 $G^{m} \circ G^{n} = G^{m + n}$ 。特别地， $G^{0}$ 为 恒等关系 $I_{V (G)}$ ，且 $G^{*} = ⋃_{i = 0}^{| V (G) |} G^{i}$ 。

显然对任意有向图，从一个节点到另一个节点的最短的路是一条通路。我们记一个图中从节点 $u$ 到节点 $v$ 的距离为从 $u$ 到 $v$ 最短通路的长度，记为 $dist (u, v)$ 。同理从一个节点出发的最短的回路是一个圈。显然对任意图，通路的最大长度为 $| V (G) | - 1$ 。

在任意图上有重要的 三角不等式 成立：

对图上任意的节点 $u$ ， $v$ ， $k$ ，有
$dist (u, v) \leq dist (u, k) + dist (k, v)$
当且仅当 $k$ 位于 $u$ 到 $v$ 的最短路上时取等。

在算法应用中，我们可能会遇到边带权的图，若将两节点的距离定义为所经过路径的权值之和，则三角不等式对于带负权的图不成立。但本节将不会考虑带权图。

对于任意两个节点 $u$ 与 $v$ ，若 $u$ 由 $v$ 可达且 $v$ 由 $u$ 可达，则我们称这两个节点是 强联通的，一系列两两强联通的节点构成了一个 强联通分量。类似路关系，我们有 强联通关系，记作 $G^{\leftrightarrow}$ ^[1]。显然 $G^{\leftrightarrow} = G^{*} \cap (G^{*})^{- 1}$ 。

前述的知识都相对 trivial。我们接下来讨论图论中的一些重要问题。

不包含圈的有向图称作 有向无环图（Directed Acyclic Graph，DAG）。DAG 可以用于描述调度问题。在这类问题中，给出所有需要完成的任务组成的任务集合，每个任务又有一个约束集合，表示在开始此任务前必须完成的任务。显然我们以任务为节点，以任务的约束关系连有向边，可以得到一张 DAG。如果没有得到 DAG，说明任务中出现了 循环依赖，从而导致给定的任务集合无法被完成。

我们希望找出一个合适的能够完成所有任务的顺序，这对应了该 DAG 中的一个 拓扑排序。DAG 的拓扑排序是图上所有节点的一个排列，满足每个节点 $v$ 在排列中出现的顺序早于所有由 $v$ 可达的所有节点。

我们称 DAG 中的节点 $v$ 是最小的，当且仅当图中任意节点均由 $v$ 可达； $v$ 是极小的，当且仅当 $v$ 从除本身外的任意节点均不可达，也即入度为 $0$ 。类似地有最大与极大，分别指一个节点可从图中任意节点达到，与无法从本节点出发达到任意其它节点，也即出度为 $0$ 。

一张 DAG 可能没有最小元素，但至少有一个极小元素，最大元素与极大元素同理。

一张 DAG 一般有多种符合要求的拓扑排序，我们可以用下面给出的一种构造拓扑排序的方法证明所有 DAG 都有拓扑排序，该方法为：

令 $T$ 为存放算法运行结果的列表，初始为空。

从 DAG 中任意取出一个极小元素 $v$ ，加入到 $T$ 中。

从 DAG 中删去节点 $v$ 及所有与之相连的边。

重复二、三步直至 DAG 为空，此时 $T$ 为所需的一种拓扑排序。

除了得到可行的任务安排顺序外，我们还希望知道能否同时并行推进一些任务以节省完成所有任务需要的总时间。假设我们可以并发执行任意数量的任务，每个任务用时相同，我们很容易得出一种基于贪心的调度方法：仿照上面给出的寻找拓扑排序的过程，每次我们将所有的最小元素对应的任务并行执行，完成后从图中删去这些元素，以此重复。我们下面精确描述一下这个过程。

我们称集合 $A$ 的 划分 $A_{1}, A_{2}, \dots, A_{n}$ 是 $A$ 的一些非空子集的集合，满足 $⋂_{i} A_{i} = \emptyset$ 且 $⋃_{i} A_{i} = A$ ，也即 $A$ 的每一个元素都在且仅在一个子集中。这些子集被称作块。给定任务集合 $T$ 与一张表示任务约束关系的 DAG，上述并行调度方法可以得到 $T$ 的一个划分 $P_{1}, P_{2}, \dots$ ，满足对任意 $i < j$ ， $P_{i}$ 中的任意元素对 $P_{j}$ 中的任意元素都是不可达的。每个块 $P_{k}$ 代表了在第 $k$ 时间并行执行的所有任务，完成所有任务所需的最低时间为块的个数，所需要的最大“处理器”数量为 $max_{i} {| P_{i} |}$ 。

图论中对其进行描述的术语如下：

我们称 DAG 中的两个节点 $u$ 与 $v$ 是 可比较的，当且仅当一个节点从另一个节点可达，也即存在有向边。一系列两两可比较的节点构成一条链，一条有限的链结束于其最大元素。对于一张 DAG 内的某个节点 $u$ ，其可能是多条链的最大元素。我们称结束于 $u$ 的最长链为到达 $u$ 的 关键通路，该链的除 $u$ 本身外的节点个数（等于链中边的个数）为 $u$ 在这张 DAG 中的深度。特别地，一张 DAG 中所有的极小元素深度为 $0$ 。每个元素在 DAG 中的深度取决于并行调度时其位于哪一个块中，具体而言 $P_{k} \equiv {e \in T ∣ depth (e) = k}$ 。对整张 DAG 来说，可以取得的最长链即为这张 DAG 的 关键通路，该链的长度即为完成这张 DAG 所规定的一系列任务及约束的时间。

与链对应，我们称一系列两两不可比的节点构成一条反链，反链中任意两个元素在 DAG 中都是不可达的。与最大链对应于完成并行调度所需要的最低时间对应，最大反链反映了完成并行调度需要的最大“处理器”数量。

我们前面提到过齐次二元关系。当我们将其与有向图进行比较时，会发现这种定义在单一集合上的二元关系的关系图恰好就是一个有向图，这表明有向图与齐次二元关系是可以相互转化的。我们自然可以通过研究有向图来研究某些具有特殊性质的二元关系。

在不加说明的情况下下文的所有二元关系默认为齐次二元关系。

我们先列举一些特殊的二元关系，为了方便阅读，我们称二元关系 $R$ 具有如下性质当且仅当对 $\forall a, b, c$

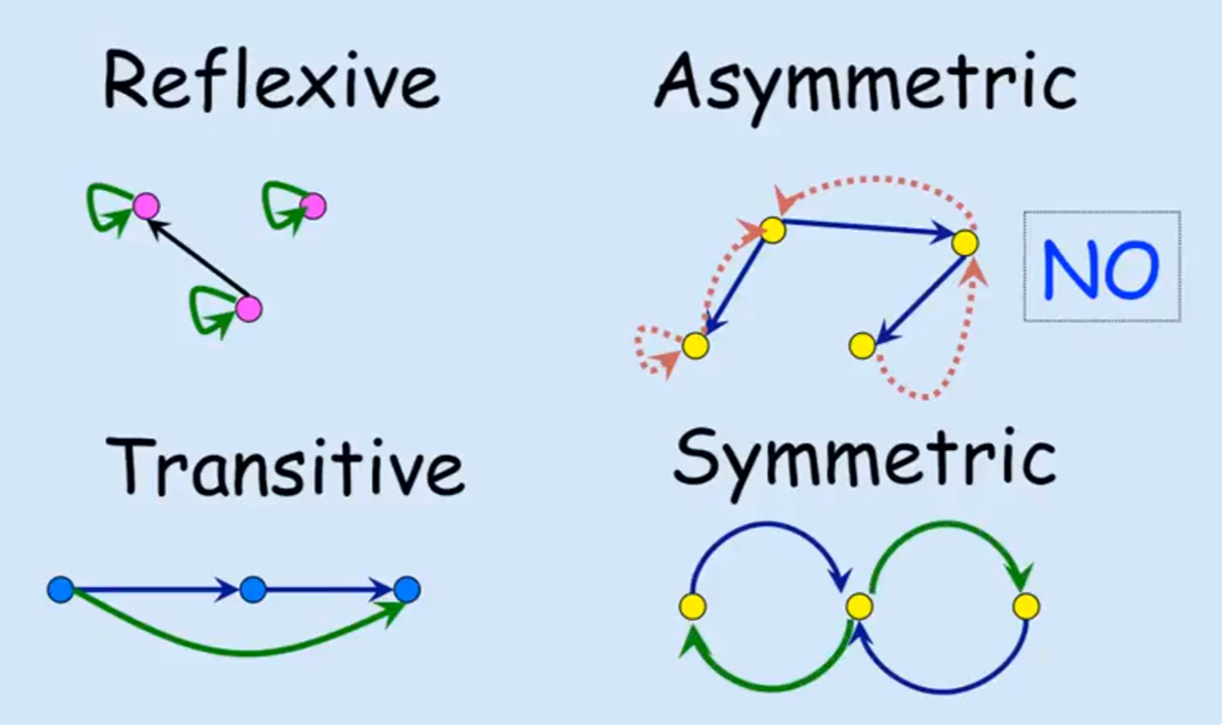
自反性（Reflexivity）： $a R a$
对称性（Symmetry）：若 $a R b$ ，则 $b R a$
传递性（Transitivity）：若 $a R b$ 且 $b R c$ ，则 $a R c$
连接性（Connectivity）：若 $a \neq b$ ，则 $(a R b) \lor (b R a)$

与这些性质相对，有

反自反性（Irreflexivity）： $\neg (a R a)$
非对称性（Asymmetry）： $(a R b) \to \neg (b R a)$
反对称性（Antisymmetry）：若 $a \neq b$ ，则 $(a R b) \to \neg (b R a)$

上述这些性质的直观展示如下：
Pasted image 20250909170426.png

具有 自反性、传递性 的二元关系 $R$ 被称作预序。

具有 自反性、反对称性、传递性 的二元关系 $R$ 被称作 弱偏序关系，有时也简单称作偏序。常用符号 $⪯$ 表示。小于等于关系 $\leq$ ，子集关系 $\subseteq$ 及与之类似的关系都是弱偏序关系。此外， $N$ 上的整除关系与恒等关系 $I$ 也是弱偏序的。具有 连接性 的弱偏序被称作全序或 线性序。小于等于关系是全序，但子集关系不是。

具有 反自反性、传递性 的二元关系 $R$ 被称作 严格偏序关系，常用符号 $≺$ 表示。其等价定义为具有传递性、非对称性。小于关系 $<$ ，真子集关系 $\subset$ 及与之类似的关系都是严格偏序关系。此外，空关系也是严格偏序的。具有 连接性 的严格偏序被称作 严格全序。小于关系是严格全序，但真子集关系不是。

具有 自反性、对称性、传递性 的二元关系 $R$ 被称作 等价关系。相等关系是最典型的等价关系，同余关系也是等价关系。等价关系与划分紧密相关，我们称一个定义在 $A$ 上的等价关系将 $A$ 划分为了多个块，每一块都被称作一个 等价类，每个等价类内的元素两两之间具有该等价关系。另一种理解等价关系本质的方式是：一个关系 $R$ 是等价关系，当且仅当存在一个全函数 $f$ ，使得对任意 $a, b$ 有 $a R b \leftrightarrow f (a) = f (b)$ 。

介绍了这么多特殊的二元关系，我们考察一下它们与前面提到过的有向图的关系。特别地，我们很容易知道如下定理成立：

二元关系 $R$ 是传递的，当且仅当其为某个有向图的 正路关系 $G^{+}$ 。对应地，任意有向图的路关系 $G^{*}$ 与正路关系 $G^{+}$ 都是传递的，与此同时路关系 $G^{*}$ 还是自反的。
有向图 $G$ 是 DAG，当且仅当 $R^{+}$ 是反自反的，依据严格偏序的两个等价定义，该性质等价于 $R^{+}$ 是非对称的。
二元关系 $R$ 是一个偏序，当且仅当其为某个有向图的 路关系 $G^{*}$ 。
二元关系 $R$ 是一个 等价关系，当且仅当其为某个有向图的 强联通关系 $G^{\leftrightarrow}$ 。
显然对于一个全序或严格全序，所有元素都是可比的，其关系图中必然存在一条长度恰为域大小的链。

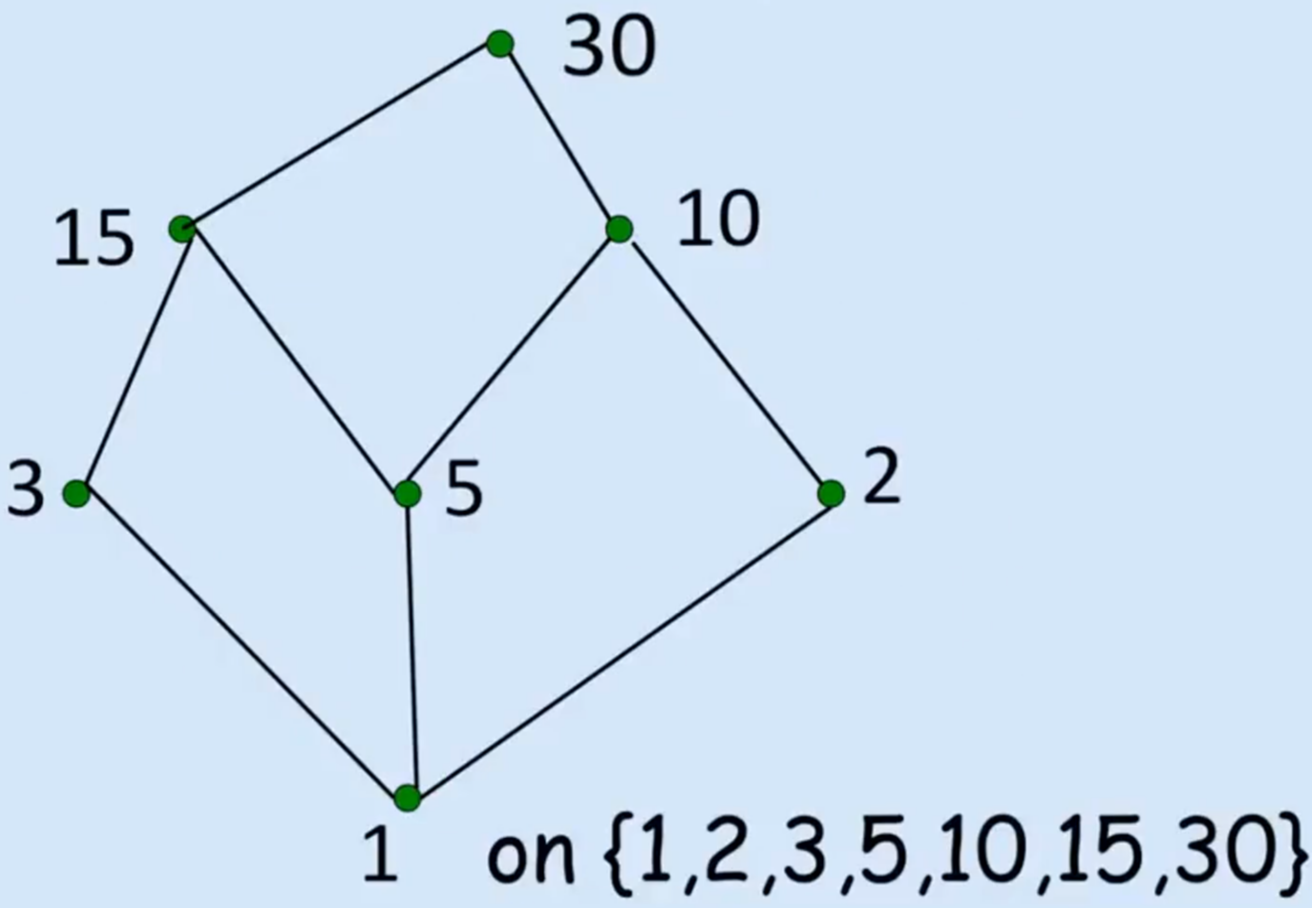
对于定义在有限集上的偏序关系，我们可以用 Hasse 图 来直观表示偏序关系。我们首先在一个偏序关系 $(S, ⪯)$ 上称 $b$ 覆盖 $a$ ，当且仅当 $a ≺ b$ 且 $∄ k \in S . a ≺ k ≺ b$ 。对有限集 $S$ 与定义在其上的偏序 $⪯$ ，其 Hasse 图为一张点集 $V = S$ ，边集 $E \equiv {⟨ u, v ⟩ \in S^{2} ∣ v 覆盖 u}$ 的有向图。

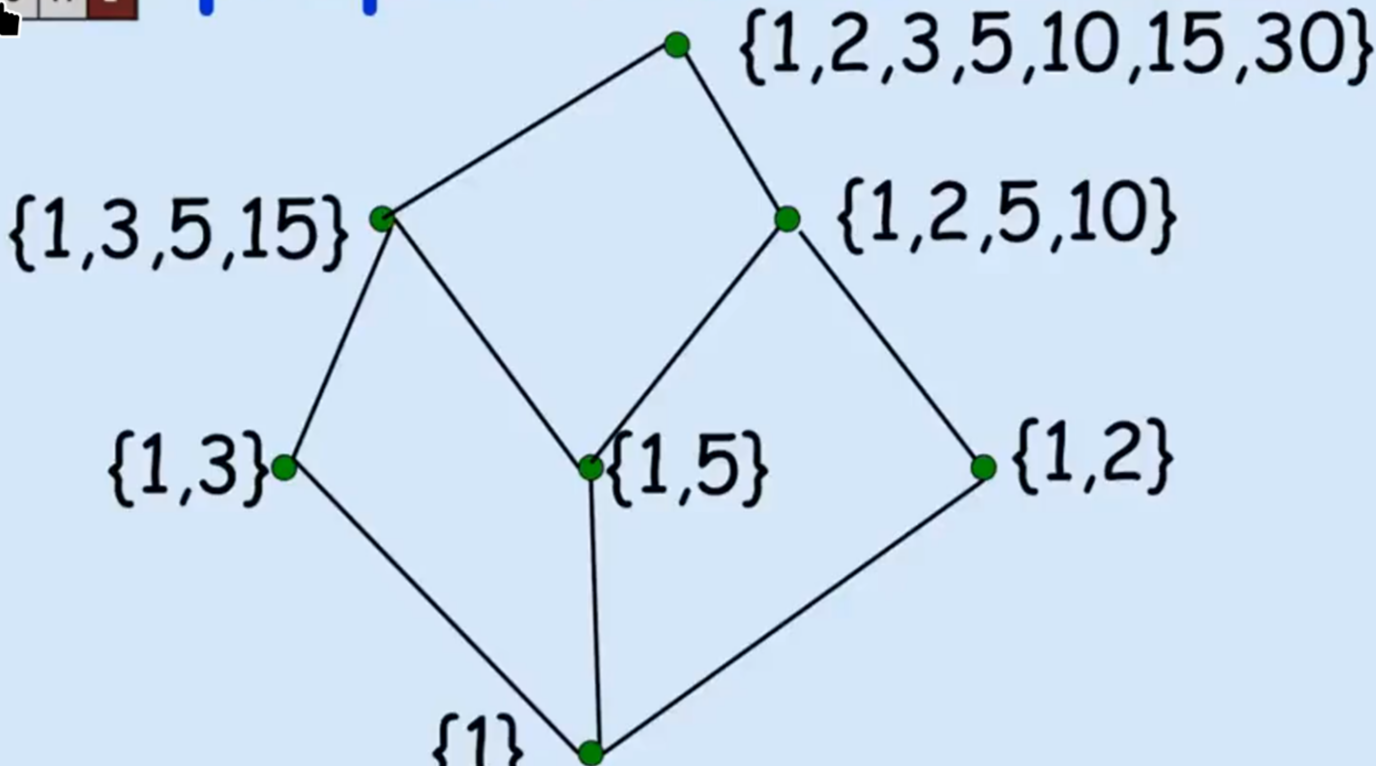
例如，这是定义在 $A = {1, 2, 3, 5, 10, 15, 30}$ 上的整除关系与定义在 $pow (A)$ 的某个子集上的真子集关系的 Hasse 图：
Pasted image 20250909163736.png
Pasted image 20250909163710.png

非常容易发现这两张 Hasse 图是同构的。这启发我们，这两个二元关系或许也是相似的。因此，仿照图同构的定义，我们称定义在 $A$ 上的二元关系 $R$ 与定义在 $B$ 上的二元关系 $S$ 是 同构的，当且仅当存在一个 $A \to B$ 的 双射 $f$ ，满足

a R b \leftrightarrow f (a) R f (b)

事实上，我们有如下定理：

每个定义在 $A$ 上的偏序 $⪯$ 都与一个定义在 $pow (A)$ 某个子集上的子集关系 $\subseteq$ 同构；对应地，严格偏序 $≺$ 都与一个定义在 $pow (A)$ 某个子集上的真子集关系 $\subset$ 同构。

证明方法十分简单，我们可以直接构造一个双射，其将 $A$ 中的每个元素 $a$ 映射 $a$ 的逆像（在 Hasse 图中就是所有“先于” $a$ 的元素）及其本身所组成的集合上。

强联通关系没有统一的标准表示，此处的符号仅为笔者的个人记号，还请留意。 ↩︎