2.6 P2P

与 CS 结构相反，P2P 结构对打开的基础设施服务器依赖要小很多或甚至不需要这些依赖，而是由成对的用户终端（被称作 对等体）直接通信。对等节点由于直接是用户的客户端，因此并不需要总是在线，每次上线时的 IP 也可以变化。

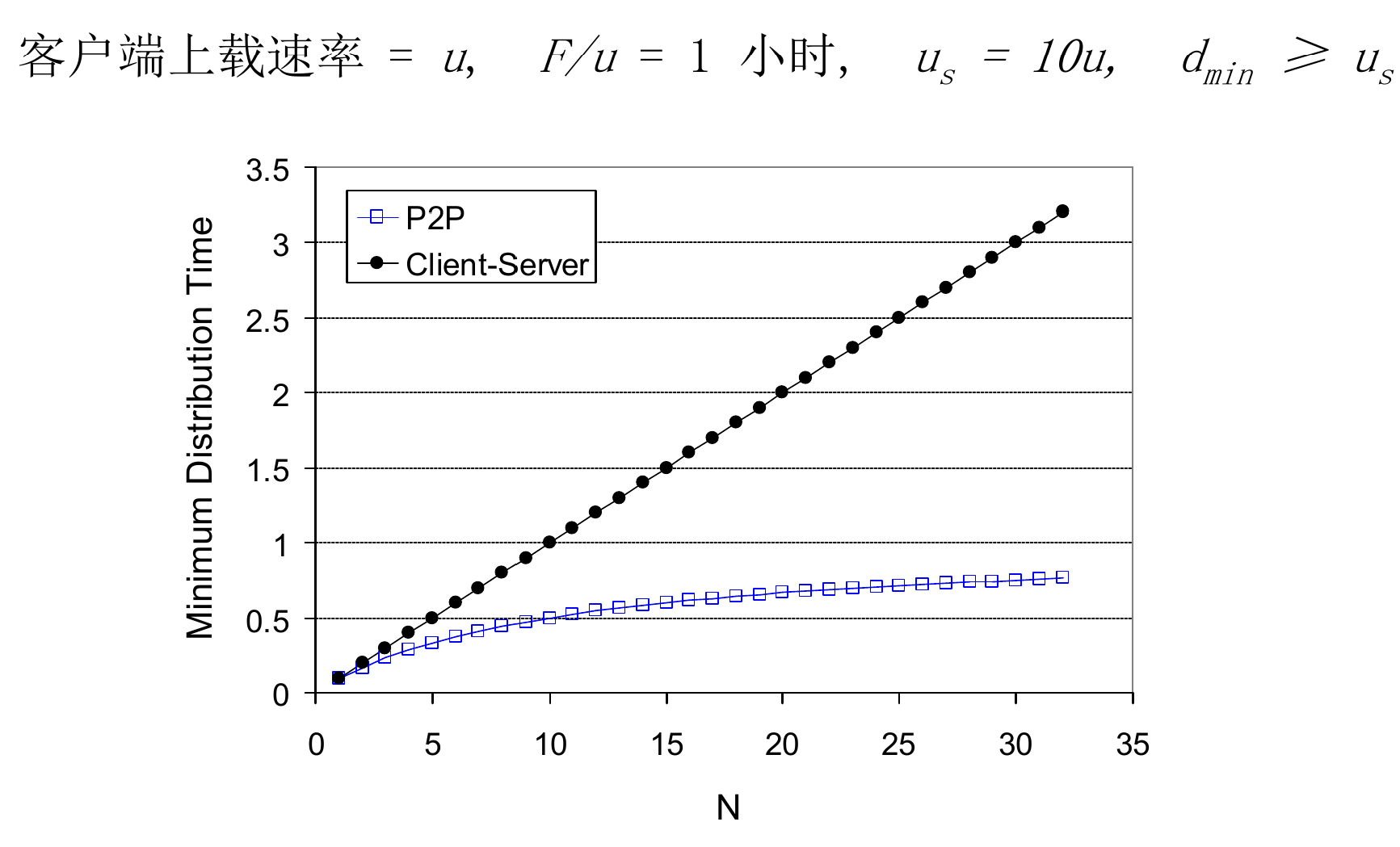
P2P 的一个最大优势便是在于其 自拓展性。我们通过一个例子大致感受一下：

假设一个由一个服务器与 $N$ 个用户终端组成的网络。服务器的上行链路传输速率为 $u$ ，第 $i$ 个用户终端的上下行链路速率分别为 $u_{i}$ ， $d_{i}$ ，现在每一个用户终端都同时需要从服务器处获取一个大小为 $L$ 的文件。在理想情况下：

如果这是一个 CS 结构的网络，则总的传输用时：

不小于服务器与 $N$ 个用户分别建立一次连接并各传输一个完整的文件副本的时间，即 $\frac{N L}{u}$ 。
不小于下载速率最低的用户下载该文件的用时，即 $\frac{L}{d_{m i n}}$ 。

综上，有总用时

t_{C S} \geq min (\frac{N L}{u}, \frac{L}{d_{m i n}})

如果这是一个 P2P 结构的网络，则总的传输用时：

不小于服务器将一份文件副本推送到这个网络中的用时，即 $\frac{L}{u}$
不小于下载速率最低的用户下载该文件的用时，即 $\frac{L}{d_{m i n}}$ 。
我们粗略地认为这个网络的总上载数据的能力为 $u + \sum_{i = 1}^{N} u_{i}$ ，该网络中至少需要流转 $N$ 份文件副本，则传输用时不小于整个网络上载所有 $N$ 份文件副本的用时，即 $\frac{N L}{u + \sum_{i = 1}^{N} u_{i}}$ 。

综上，有总用时

t_{P 2 P} \geq min (\frac{L}{u}, \frac{L}{d_{m i n}}, \frac{N L}{u + \sum_{i = 1}^{N} u_{i}})

当 $N$ 足够大，而每个用户的下载速率与上传速率 $u_{i}$ 与 $d_{i}$ 近似相等时，可以发现 CS 结构网络中最短用时将呈线性增长。而在 P2P 结构下，每个新增节点的加入在带来更多需求的同时也带来了更多服务能力，最短用时的增长趋势要慢于 CS 模式。

Pasted image 20250324151710.png

P2P 的网络结构

P2P 的网络结构可以细分为 非结构化 P2P 与 结构化 P2P 两种。前者根据其对中心基础服务器的依赖程度又可分为 集中式、分散式、半分散式。下面我们各举一例进行讲解：

集中式：Napster

存在一个 中心目录服务器。对等方通过与该中心目录服务器通信，告知本机的 IP 地址与拥有的文件，并从中心服务器获取网络中所有在线主机拥有文件的目录与存储某个特定文件主机的 IP 地址。主机获取到相应的 IP 地址后就可以与对方通信，请求响应的文件。
文件的存储与传输是分散的，但目录查询与定位是集中式的。
中心的目录服务器仍然无法避免诸如单点故障、性能瓶颈、远距离客户端的响应延迟等问题。

分散式：Gnutella

本部分所介绍的内容已经过时，基本不再被现代工业界所使用。

无需任何中心服务器。
定义所有活动的对等体与它们之间建立的连接为 覆盖网络（Overlay Network）。网络中的节点代表对等体，边代表对等体之间建立的 逻辑上 的应用层连接。
泛洪（Flooding） 查询：对等体向其所有邻居发送查询请求，邻居收到查询请求后，若自身不存在所需的文件，再向该邻居的所有邻居（除源请求方外）发送查询请求，使得查询请求逐渐遍布全网。查找到结构后，再按查询请求传播的相反的顺序应答查询请求。为了防止查询请求在网络中无休止的回荡甚至增强，例如设置 TTL、请求标号等。
加入网络：对等体有一张 可用对等体列表，列举了极有可能在线的对等体的 IP 地址。对等体试图向表中的对等体发送 Ping 报文。所有收到 Ping 报文的对等方继续向其他地方转发 Ping 报文，并向源主机返回 Pong 报文，包含了本机的 IP 地址、共享文件的情况等。如同石头丢入水面一般源主机获知了这个网络中大量的在线对等体的列表，再根据协议挑选一些对等题建立直接的 TCP 连接。

混合式：KaZaA

对等体分为两类：组长或隶属于某个组长的节点。组长之间有 TCP 连接。组长再与管辖的组员进行 TCP 连接，并维护该组内的所有内容。
每个文件有一个散列标识码（通过哈希算法生成）与一个描述符。
组员向组长发送文件查询请求，组长首先在组内查询结果，若组内没有匹配的结果再转发给其它组长查询。组长使用一个形如 <元数据, 散列标识码, IP 地址> 的匹配进行响应。客户端响应后，就可以根据结果建立 TCP 连接下载对应文件。
KaZaA 存在请求排队、激励优先权、并行下载等机制。

结构化 P2P：分布式散列表（DHT）

有意建立一个特殊的拓扑结构（如环、树）便于查询。
每个节点维护整个散列表的一个特定区域。

P2P 系统实例：BitTorrent

称参与一个特定文件分发的所有对等方的集合被称为一个 洪流（Torrent）。文件以 256KB 一块（Chunk） 的大小传输。每个洪流存在一个基础设施节点——追踪器（tracker），负责维护洪流中的对等方的信息。每个对等体需要与追踪器建立连接，注册一些信息后并从追踪器得到该洪流中的节点列表，才算加入某个洪流。

某个对等体加入一个洪流并请求一个文件时，一般而言它上来没有该文件的任何一块。它于是与该洪流中的其它节点发送请求。随着时间流逝，该节点会获得一些文件块，此时它也可以根据自身现有的文件块接受其他人的请求。

请求块的机制：最稀缺优先（Rarest First）。对等体周期性向邻居询问拥有块的信息（获取位图），并请求目前最稀有（副本数量最少）的块，以期大致均衡每个块在洪流中的数量。

发送块的机制：一报还一报（Tit-for-tat）。根据最近一个周期（一般为 30 秒）内为自己提供了最大传输速率的几位邻居，主动先向他们建立连接传输对方所需要的块。每过一个周期，随机再选择一个其它节点并向对方提供服务，以期找到更好的传输伙伴。

其它机制：例如流水线、随机优先选择、残局模型与反怠慢，详情见 Wikipedia。